Write an algebraic expression for each verbal expression – In the realm of mathematics, algebraic expressions play a pivotal role in representing mathematical concepts and relationships. They provide a concise and symbolic way to express numerical operations and quantities. This guide delves into the intricacies of algebraic expressions, exploring their definition, types, and the process of translating verbal expressions into their algebraic counterparts.
Algebraic expressions form the foundation for more complex mathematical concepts, enabling the representation of real-world scenarios and the exploration of mathematical patterns. By understanding the principles of algebraic expressions, individuals can develop a deeper understanding of mathematical operations and their applications in various fields.
Algebraic Expressions: Write An Algebraic Expression For Each Verbal Expression

An algebraic expression is a mathematical phrase that combines numbers, variables, and operations. It represents a mathematical relationship or quantity without specifying a specific value.
For example, 2x + 3, 5(y – 1), and 3z^2 – 5z + 2 are all algebraic expressions.
Types of Algebraic Expressions
- Monomial:An algebraic expression with only one term, such as 2x or 5y^2.
- Binomial:An algebraic expression with two terms, such as 2x + 3 or 5(y – 1).
- Trinomial:An algebraic expression with three terms, such as 3z^2 – 5z + 2.
- Polynomial:An algebraic expression with more than three terms, such as 2x^3 + 5x^2 – 3x + 1.
Verbal Expressions
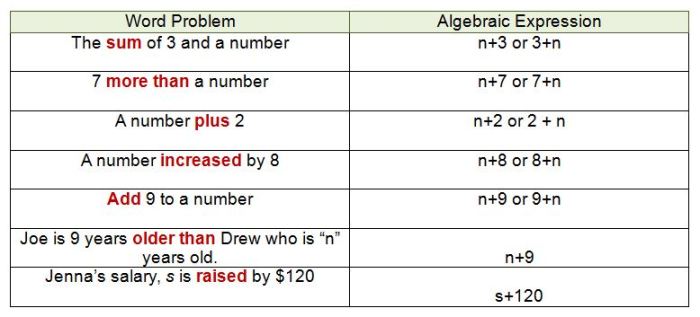
A verbal expression is a mathematical phrase written in words. It describes a mathematical relationship or quantity without using mathematical symbols.
For example, “the sum of two numbers” or “five times the difference between a number and one” are both verbal expressions.
Identifying Key Elements of a Verbal Expression, Write an algebraic expression for each verbal expression
To translate a verbal expression into an algebraic expression, it is important to identify the following key elements:
- Variables:The unknown quantities in the expression.
- Operations:The mathematical operations used in the expression, such as addition, subtraction, multiplication, and division.
- Constants:The fixed numbers in the expression.
Translating Verbal Expressions into Algebraic Expressions

To translate a verbal expression into an algebraic expression, follow these steps:
- Identify the variables:Assign a variable to each unknown quantity in the expression.
- Translate the operations:Use mathematical symbols to represent the operations in the expression.
- Combine the variables and operations:Put the variables and operations together to form an algebraic expression.
Common Challenges
Some common challenges when translating verbal expressions include:
- Identifying the variables:It is important to be clear about what each variable represents.
- Translating the operations:Some operations may be implied in a verbal expression, so it is important to be careful when translating them.
- Combining the variables and operations:It is important to use the correct order of operations when combining the variables and operations.
Examples

| Verbal Expression | Algebraic Expression | Explanation |
|---|---|---|
| The sum of two numbers | x + y | Let x and y be the two numbers. |
| Five times the difference between a number and one | 5(x – 1) |
Let x be the number. |
| The area of a rectangle with length 2x and width y | 2xy | The area of a rectangle is length times width. |
| The volume of a cube with side length s | s^3 | The volume of a cube is side length cubed. |
| The distance traveled in t hours at a speed of v miles per hour | vt | Distance equals speed times time. |
| The perimeter of a square with side length x | 4x | The perimeter of a square is four times the side length. |
| The circumference of a circle with radius r | 2πr | The circumference of a circle is 2π times the radius. |
| The slope of a line passing through points (x1, y1) and (x2, y2) | (y2 – y1) / (x2 – x1) |
The slope of a line is the change in y divided by the change in x. |
| The equation of a line with slope m and y-intercept b | y = mx + b | The equation of a line is y equals mx plus b, where m is the slope and b is the y-intercept. |
| The quadratic equation with roots r1 and r2 | (x – r1)(x – r2) = 0 |
The quadratic equation with roots r1 and r2 is the product of the factors (x – r1) and (x – r2). |
FAQ Insights
What is the difference between an algebraic expression and a verbal expression?
An algebraic expression uses mathematical symbols and operations to represent a mathematical concept, while a verbal expression uses words to describe a mathematical concept.
How do I identify the key elements of a verbal expression?
Look for s that indicate mathematical operations (e.g., plus, minus, times, divided by) and quantities (e.g., numbers, variables).
What are some common challenges in translating verbal expressions into algebraic expressions?
Challenges may include identifying implied operations, dealing with complex verbal expressions, and ensuring the algebraic expression accurately reflects the verbal expression.