Which of the following integrals are improper? This question marks the commencement of an in-depth exploration into the fascinating realm of improper integrals. As we delve into this mathematical domain, we will unravel the intricacies of convergence and divergence, discover techniques for evaluating improper integrals, and uncover their diverse applications in fields beyond mathematics.
From the convergence test to step-by-step procedures for evaluation, this comprehensive guide equips readers with a thorough understanding of improper integrals. We will also venture into the practical applications of improper integrals, showcasing their significance in solving real-world problems.
Definitions and Types of Improper Integrals

Improper integrals are a class of integrals where the integrand is unbounded or the interval of integration is infinite. They extend the concept of definite integrals to handle functions that have infinite values or extend over infinite intervals.
Improper integrals are classified into two main types:
- Type I:Integrals with an infinite interval of integration
- Type II:Integrals with an unbounded integrand
Criteria for Convergence and Divergence

The convergence or divergence of an improper integral determines whether it has a finite value or not.
Convergence Test:If the limit of the integrand as the interval approaches infinity is finite, the improper integral converges. Otherwise, it diverges.
Divergence Test:If the integral of the absolute value of the integrand diverges, the improper integral also diverges.
Evaluation of Improper Integrals
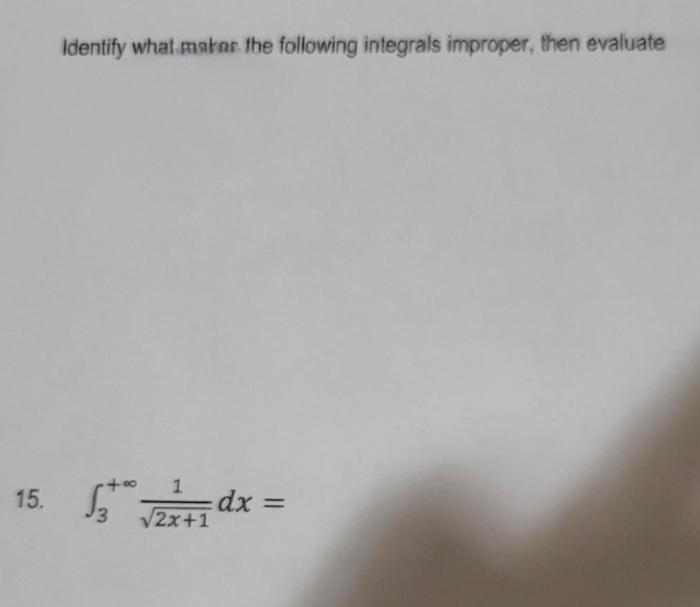
Evaluating improper integrals involves finding their limits. For Type I integrals, the limit is taken as the interval approaches infinity. For Type II integrals, the limit is taken as the integrand approaches infinity or negative infinity.
Type I Integrals:
- If the limit exists, the improper integral converges and its value is the limit.
- If the limit does not exist or is infinite, the improper integral diverges.
Type II Integrals:
- If the limit exists, the improper integral converges and its value is the limit.
- If the limit does not exist or is infinite, the improper integral diverges.
Applications of Improper Integrals

Improper integrals find applications in various fields, including:
- Calculus:Calculating volumes, areas, and lengths of regions with infinite boundaries
- Probability:Evaluating probability distributions and finding probabilities of events
- Physics:Modeling physical phenomena such as heat flow and wave propagation
Common Errors and Pitfalls: Which Of The Following Integrals Are Improper
Common mistakes when dealing with improper integrals include:
- Assuming convergence without checking the convergence test
- Evaluating improper integrals as if they were definite integrals
- Ignoring the absolute value when evaluating Type II integrals
To avoid these errors, it is essential to carefully apply the convergence and divergence tests and follow the proper procedures for evaluating improper integrals.
Popular Questions
What are the different types of improper integrals?
Improper integrals can be classified into two main types: Type I and Type II. Type I improper integrals involve an infinite limit of integration, while Type II improper integrals involve an integrand that becomes infinite at some point within the interval of integration.
How do you determine if an improper integral converges or diverges?
To determine the convergence or divergence of an improper integral, you can use the convergence test. This test involves evaluating the limit of the integrand as the limit of integration approaches infinity. If the limit is finite, the integral converges.
If the limit is infinite or does not exist, the integral diverges.
What are some common applications of improper integrals?
Improper integrals have a wide range of applications in various fields, including calculus, probability, and physics. In calculus, improper integrals are used to find the area under curves that extend to infinity. In probability, improper integrals are used to calculate probabilities of continuous random variables.
In physics, improper integrals are used to solve problems involving infinite series and Fourier transforms.